Las funciones polinómicas, exponenciales, racionales, con radicales, logarítmicas y trigonométricas son continuas en todos los puntos de sus dominios.
Continuidad de una función en un punto:
 tal que para toda X en el dominio de la función:
tal que para toda X en el dominio de la función: 
Esto se puede escribir en términos de límites de la siguiente manera:
Si x0 es punto de acumulación del dominio de la función entonces f es continua en x0 si y sólo si . Cuando x0 no es de acumulación del dominio, la función es continua en ese punto.
. Cuando x0 no es de acumulación del dominio, la función es continua en ese punto.
En el caso de aplicaciones de en
en  , y de una manera más rigurosa se dice que una función
, y de una manera más rigurosa se dice que una función  es continua en un punto x1 si existe f (x1), si existe el límite de f (x) cuando x tiende hacia x1 por la derecha, si existe el límite de f (x) cuando x tiende hacia x1 por la izquierda, y además ambos coinciden con f (x1).
es continua en un punto x1 si existe f (x1), si existe el límite de f (x) cuando x tiende hacia x1 por la derecha, si existe el límite de f (x) cuando x tiende hacia x1 por la izquierda, y además ambos coinciden con f (x1).
Si x0 es punto de acumulación del dominio de la función entonces f es continua en x0 si y sólo si
 . Cuando x0 no es de acumulación del dominio, la función es continua en ese punto.
. Cuando x0 no es de acumulación del dominio, la función es continua en ese punto.En el caso de aplicaciones de
 en
en  , y de una manera más rigurosa se dice que una función
, y de una manera más rigurosa se dice que una función  es continua en un punto x1 si existe f (x1), si existe el límite de f (x) cuando x tiende hacia x1 por la derecha, si existe el límite de f (x) cuando x tiende hacia x1 por la izquierda, y además ambos coinciden con f (x1).
es continua en un punto x1 si existe f (x1), si existe el límite de f (x) cuando x tiende hacia x1 por la derecha, si existe el límite de f (x) cuando x tiende hacia x1 por la izquierda, y además ambos coinciden con f (x1).
Continuidad lateral:
Una función  es continua por la izquierda en el punto
es continua por la izquierda en el punto  si el límite lateral por la izquierda y el valor.de la función en el punto son iguales. Es decir:
si el límite lateral por la izquierda y el valor.de la función en el punto son iguales. Es decir:
 es continua por la izquierda en el punto
es continua por la izquierda en el punto  si el límite lateral por la izquierda y el valor.de la función en el punto son iguales. Es decir:
si el límite lateral por la izquierda y el valor.de la función en el punto son iguales. Es decir:
Una función
 es continua por la derecha en el punto
es continua por la derecha en el punto  si su límite lateral por la derecha y el valor de la función en el punto son iguales. Es decir:
si su límite lateral por la derecha y el valor de la función en el punto son iguales. Es decir: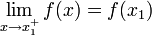
Una función
 es continua en un punto si es continua por la izquierda y es continua por la derecha. Esto es:
es continua en un punto si es continua por la izquierda y es continua por la derecha. Esto es:
Continuidad de una función en un intervalo abierto (a,b):

Una función, f es continua en un intervalo abierto I= (a,b), si y solo si la función es continua en todos los puntos del intervalo, es decir:

Continuidad de una función en un intervalo cerrado [a,b]:

Una función f es continua en un intervalo cerrado [a, b] si la función es continua en el intervalo abierto (a,b) y es continua por la derecha de a y continua por la izquierda de b:
Falta la bibliografía.
ResponderEliminar+1
Eliminar